Building a maths curriculum for a world shaped by computing
In the penultimate seminar in our series on cross-disciplinary computing, we were delighted to host Conrad Wolfram (European co-founder/CEO of Wolfram Research).

Conrad has been an influential figure in the areas of AI, data science, and computation for over 30 years. The company he co-founded, Wolfram Research, develops computational technologies including the Wolfram programming language, which is used by the Mathematica and WolframAlpha programs. In the seminar, Conrad spoke about his work on developing a mathematics curriculum “for the AI age”.

Computation is everywhere
In his talk, Conrad began by talking about the ubiquity of computation. He explained how computation (i.e. an operation that follows conditions to give a defined output) has transformed our everyday lives and led to the development of entire new sub-disciplines, such as computational medicine, computational marketing, and even computational agriculture. He then used the WolframAlpha tool to give several practical examples of applying high-level computation to problem-solving in different areas.
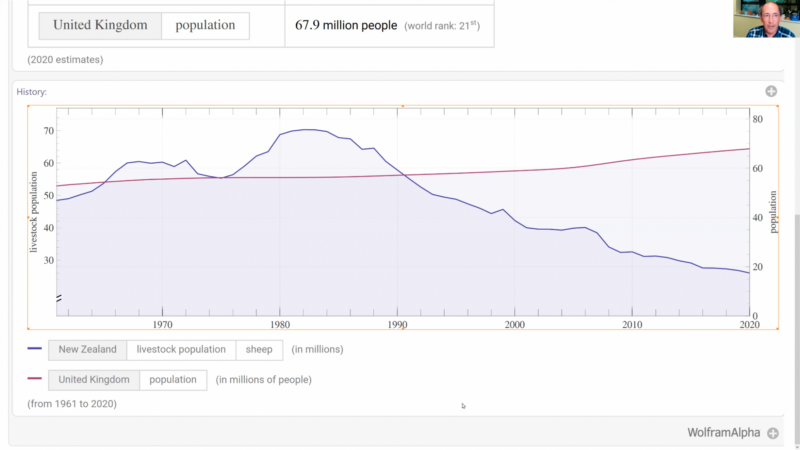
The power of computation for mathematics
Conrad then turned his attention to the main question of his talk: if computation has also changed real-world mathematics, how should school-based mathematics teaching respond? He suggested that, as computation has impacted all aspects of our daily lives, school subjects should be reformed to better prepare students for the careers of the future.
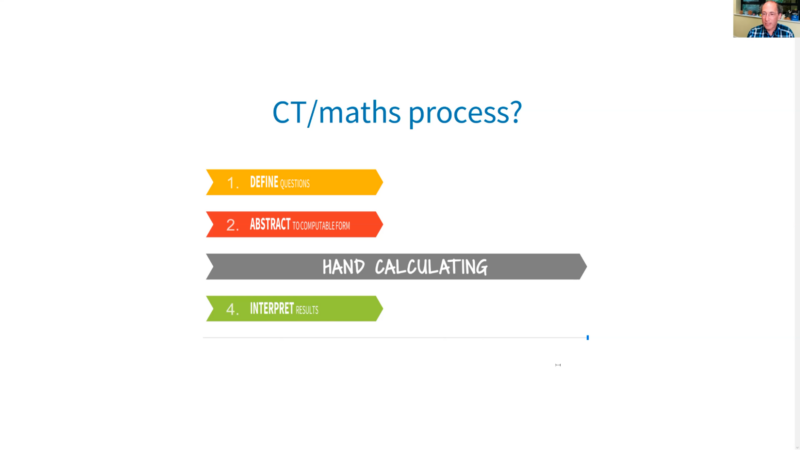
His biggest criticism was the use of hand calculation methods in mathematics teaching. He proposed that a mathematics curriculum that “assumes computers exist” and uses computers (rather than humans) to compute answers would better support students to develop a deep understanding of mathematical concepts and principles. In other words, if students spent less time doing hand-calculation methods, they could devote more time to more complex problems.
What does computational problem-solving look like?
One interesting aspect of Conrad’s talk was how he modelled the process of solving problems using computation. In all of the example problems, he outlined that computational problem-solving follows the same four-step process:
- Define the question: Students think about the scope and details of the problem and define answerable questions to tackle.
- Abstract to computable form: Using the information provided, students translate the question into a precise abstract form, such as a diagram or algorithm, so that it can be solved by a computer-based agent.
- Computer answers: Using the power of computation, students solve the abstract question and resolve any issues during the computation process.
- Interpret results: Students reinterpret and recontextualise the abstract answer to derive useful results. If problems emerge, students refine or fix their work.
Depending on the problem, the process can be repeated multiple times until the desired solution is reached. Rather than being proposed as a static list of outcomes, the process was presented by Conrad as an iterative cycle than resembles an “ascending helix”:
A curriculum for a world with AI
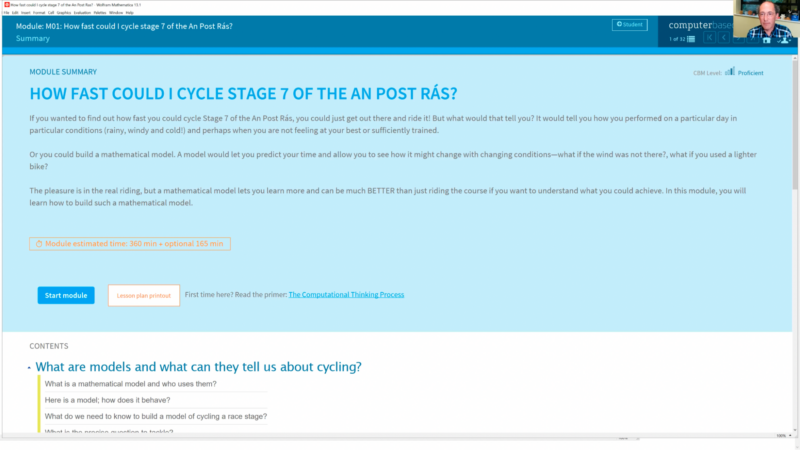
In the later stages of his talk, Conrad talked about the development of a new computational curriculum to better define what a modern mathematics curriculum might look like. The platform that hosts the curriculum, named Computer-Based Math (or CBM), outlines the need to integrate computational thinking into mathematics in schools. For instance, one of the modules, How Fast Could I Cycle Stage 7 Of The An Post Rás?, asks students to develop a computational solution to a real-world problem. Following the four-step problem-solving process, students apply mathematical models, computational tools, and real-world data to generate a valid solution:
Some future challenges he remarked on included how a computer-based mathematics curriculum could be integrated with existing curricula or qualifications, at what ages computational mathematics should be taught, and what assessment, training, and hardware would be needed to support teachers to deliver such a curriculum.
Conrad concluded the talk by arguing that the current need for computational literacy is similar to the need for mass literacy and pondering whether the UK could lead the push towards a new computational curriculum suitable for learners who grow up with AI technologies. This point provided food for thought during our discussion section, especially for teachers interested in embedding computation into their lessons, and for researchers thinking about the impact of AI in different fields. We’re grateful to Conrad for speaking about his work and mission — long may it continue!
You can catch up on Conrad’s talk with his slides and the talk’s recording:
More to explore
Conrad’s book, The Math(s) Fix: An Education Blueprint for the AI Age, gives more details on how he thinks data science, AI, and computation could be embedded into the modern maths curriculum.
You can also explore Wolfram Research’s Computer-Based Maths curriculum, which offers learning materials to help teachers embed computation in their maths lessons.
Finally, try out Wolfram’s tools to solve everyday problems using computation. For example, you might ask WolframAlpha data-rich questions, which the tool converts from text input into a computable problem using natural language processing. (Two of my favourite example questions are: “How old was Leonardo when the Mona Lisa was painted?” and “What was the weather like when I was born?”)
Join our next seminar
In the final seminar of our series on cross-curricular computing, we welcome Dr Tracy Gardner and Rebecca Franks (Raspberry Pi Foundation) to present their ongoing work on computing education in non-formal settings. Sign up now to join us for this session on Tues 8 November:
We will shortly be announcing the theme of a brand-new series of research seminars starting in January 2023. The seminars will take place online on the first Tuesday of the month at 17:00–18:30 UK time.







No comments